What if a single, simple rule could generate a universe of infinite complexity? That’s the paradox and the promise of fractal art, a mesmerizing blend of mathematics and creativity. In the world of creative coding, where tools like p5.js, TouchDesigner, and Processing give digital artists a canvas of pure possibility, fractals are the ultimate playground.
More than just a geometric curiosity, fractals are the fundamental patterns that shape everything from branching trees to swirling galaxies. They are infinitely complex, yet they can be built from surprisingly simple rules, making them a perfect fit for artists who love to code.
What Makes a Fractal Tick?
Mathematician Benoît Mandelbrot coined the term “fractal” to describe shapes with a unique property called self-similarity: no matter how much you zoom in, you’ll find smaller copies of the whole pattern repeating endlessly.
Think of it like a Russian doll, but instead of dolls, it’s patterns within patterns. This is the core magic behind fractals. Unlike a simple line or square, fractals exist in fractional dimensions—more complex than a line but less than a plane. This is what gives them their incredible richness and detail.
The real secret to building them is iteration, or applying a simple rule over and over again. Start with a basic shape, transform it, then apply the same transformation to the new result. Each loop adds a new layer of complexity, building intricate patterns that would be impossible to create by hand.
Nature’s Blueprint
You don’t have to look far to find fractals in the wild. They’re everywhere, from the branching patterns of a tree to the delicate spirals of a pinecone. Your own body is a testament to their efficiency; your lungs and blood vessels are fractal networks that maximize surface area in a compact space.
Even randomness can lead to fractal beauty. The branching patterns of lightning are fractals formed as electricity seeks the path of least resistance. The intricate shapes of coastlines are fractals too—the closer you look, the more detail you find.

Getting Started with p5.js Fractals
The beauty of p5.js is how it makes these complex ideas accessible. Its recursive functions are perfect for creating self-similar patterns. With just a few lines of code, you can bring these mathematical wonders to life.
Your First Fractal Tree
A recursive tree is the perfect place to start. Each branch splits into two smaller branches, each a bit shorter and angled differently from its parent. The drawBranch function calls itself, creating a new generation of branches with each iteration.
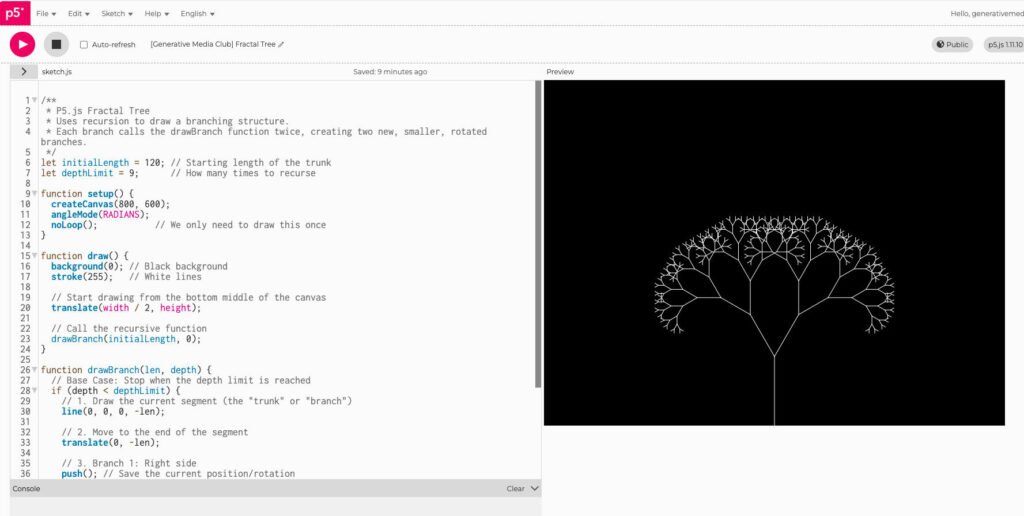
/**
* P5.js Fractal Tree
* Uses recursion to draw a branching structure.
* Each branch calls the drawBranch function twice, creating two new, smaller, rotated branches.
*/
let initialLength = 120; // Starting length of the trunk
let depthLimit = 9; // How many times to recurse
function setup() {
createCanvas(800, 600);
angleMode(RADIANS);
noLoop(); // We only need to draw this once
}
function draw() {
background(0); // Black background
stroke(255); // White lines
// Start drawing from the bottom middle of the canvas
translate(width / 2, height);
// Call the recursive function
drawBranch(initialLength, 0);
}
function drawBranch(len, depth) {
// Base Case: Stop when the depth limit is reached
if (depth < depthLimit) {
// 1. Draw the current segment (the "trunk" or "branch")
line(0, 0, 0, -len);
// 2. Move to the end of the segment
translate(0, -len);
// 3. Branch 1: Right side
push(); // Save the current position/rotation
rotate(PI / 6); // Rotate 30 degrees (PI/6)
drawBranch(len * 0.7, depth + 1); // Recurse with 70% of the length
pop(); // Restore position/rotation
// 4. Branch 2: Left side
push(); // Save the current position/rotation
rotate(-PI / 6); // Rotate -30 degrees
drawBranch(len * 0.7, depth + 1); // Recurse with 70% of the length
pop(); // Restore position/rotation
}
}The Hypnotic Koch Snowflake
The Koch snowflake is a mathematical marvel with a finite area but an infinite perimeter. You start with a triangle and on each side, you remove the middle third and add a smaller triangular bump. You repeat this process forever, creating an impossibly detailed shape.
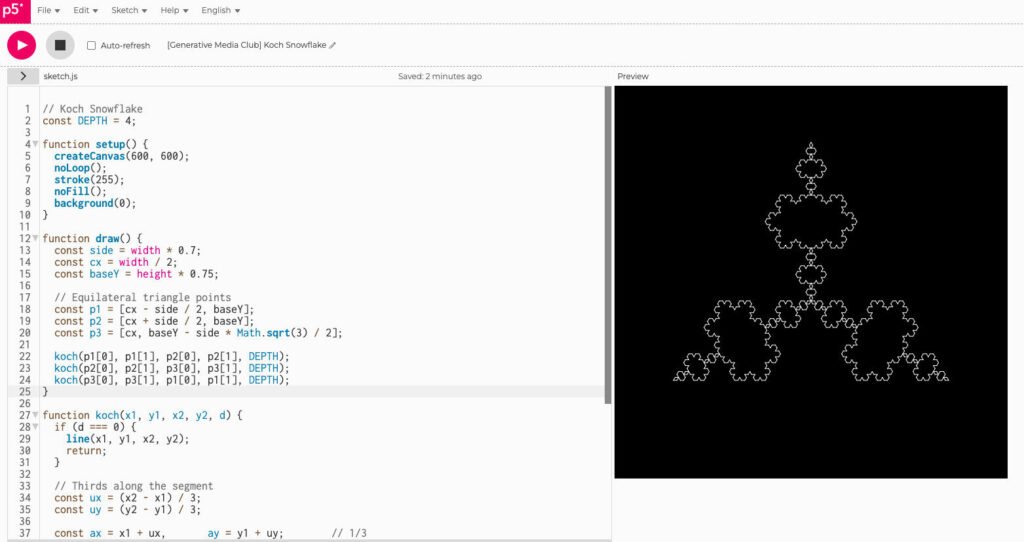
// Koch Snowflake
const DEPTH = 4;
function setup() {
createCanvas(600, 600);
noLoop();
stroke(255);
noFill();
background(0);
}
function draw() {
const side = width * 0.7;
const cx = width / 2;
const baseY = height * 0.75;
// Equilateral triangle points
const p1 = [cx - side / 2, baseY];
const p2 = [cx + side / 2, baseY];
const p3 = [cx, baseY - side * Math.sqrt(3) / 2];
koch(p1[0], p1[1], p2[0], p2[1], DEPTH);
koch(p2[0], p2[1], p3[0], p3[1], DEPTH);
koch(p3[0], p3[1], p1[0], p1[1], DEPTH);
}
function koch(x1, y1, x2, y2, d) {
if (d === 0) {
line(x1, y1, x2, y2);
return;
}
// Thirds along the segment
const ux = (x2 - x1) / 3;
const uy = (y2 - y1) / 3;
const ax = x1 + ux, ay = y1 + uy; // 1/3
const cx = x1 + 2 * ux, cy = y1 + 2 * uy; // 2/3
// Rotate (ux, uy) by -60° using 2D rotation formulas
const cos60 = 0.5, sin60 = Math.sqrt(3) / 2;
const rx = ux * cos60 + uy * sin60; // cos(-60)=cos60, -sin(-60)=+sin60
const ry = -ux * sin60 + uy * cos60; // sin(-60) = -sin60
const bx = ax + rx, by = ay + ry; // tip point
d--;
koch(x1, y1, ax, ay, d);
koch(ax, ay, bx, by, d);
koch(bx, by, cx, cy, d);
koch(cx, cy, x2, y2, d);
}
The Infinite Journey
Fractal art offers an infinite creative path. Start with these basic shapes, then experiment with colors, animations, and interactions. The journey from simple rules to complex beauty mirrors the fractals themselves—each step builds on the previous, creating something far greater than the sum of its parts.
Whether you’re a seasoned creative coder or just starting out, there’s a fractal waiting for you. Dive in, experiment, and see what wonders you can generate with just a few lines of code.
What’s the first fractal you want to create?


















